How to Apply BODMAS Rules of Arithmetic to Microsoft® Excel Formulas
Last updated on 2024-05-23.
“I'm No Good at Maths”
Since 1989 I've given Excel training to about 2,000 people working for about 200 businesses ranging in size from SMEs to multi-nationals.
Scores of those people said to me “I'm no good at maths” or words to that effect. I recall only one for whom I failed to shake from that belief.
My thought on hearing this claim is that the person making it is nothing of the sort. I can only guess at where they got that unfortunate notion into their head.
Now, I must qualify what we mean by “maths” in the context of this article and of using Excel in the office.

We're talking about oranges and apples; about pounds, shillings and pence; about dollars and cents; about quantities and unit prices; about lengths and breadths.
![]() We're not talking about finding solutions to the time-dependent Schrödinger equation.
We're not talking about finding solutions to the time-dependent Schrödinger equation.
Where to Start
You have six oranges and nine apples to share out between three girls and two boys so that each kid gets the same number of pieces of fruit. How many pieces of fruit does each kid get?
I bet your handouts won't short-change any kid in your group.
To work out the share, you perhaps placed the fruit on the table and shuffled it into five equally-sized groups.
Or you instinctively did some arithmetic:
- Three girls and two boys is five kids
- Six oranges and nine apples is 15 pieces of fruit
- Divide 15 by five makes three pieces of fruit for each kid.
No uncertainty over the arithmetic there, then? So why any doubt over your ability to do the maths?
I suspect that doubt arises when you come to translate the question of the share out of fruit as expressed in conversational English into a mathematical expression that a computer would process satisfactorily.
You're thinking “number of pieces of fruit divided by number of kids”. That is literally:
six plus nine divided by three plus two
Now, you try to use Excel to calculate the share out for you by typing this expression into a cell in an Excel spreadsheet (starting with the = to tell Excel "here comes a calculation"):
=6+9/3+2
And what does Excel advise you is the number of pieces of fruit each kid should get?
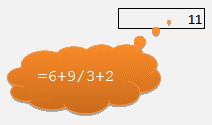
💥 WHAT THE ... ? 💥
💥 ELEVEN ... ! 💥
Here, I believe, is where any anxiety you have over doing the maths arises. You're not confident in your understanding of why Excel disagrees with your assessment that each kid should get three pieces of fruit.
In my opinion, this lack of confidence is not due to any innate lack of ability on your part to do the maths: it's due to the gap in your knowledge of the basic rules of arithmetic.
(Dare I suggest you were checking your social media when you really should have been listening to teacher?)
What you need is a little guidance from ★ BODMAS ★.
BODMAS
Consider an expression 6+9/3+2 that you want to evaluate. You read it from left to right. However, to evaluate it, you must put it into the order in which maths evaluates it.
BODMAS is a guide to the order in which the elements of an arithmetic expression, or formula, are evaluated according to the rules and language of arithmetic.
BODMAS is an acronym for Brackets Order Division Multiplication Addition Subtraction:

The order of priority is from the top down: anything within brackets must be worked out first; and so on down the list.
BUT …
There are two things that make the application of BODMAS not quite as straightforward as the above listing make it appear:
- Division and Multiplication are equal in priority to each other. So, it makes no difference if you divide before you multiply —
- Addition and Subtraction are equal in priority to each other. So, it makes no difference if you subtract before you add —
| 8*4/2 | OR | 8*4/2 |
| ⇓ | ⇓ | |
| 32/2 | 8*2 | |
| ⇓ | ⇓ | |
| 16 | 16 |
| 8+4-2 | OR | 8+4-2 |
| ⇓ | ⇓ | |
| 12-2 | 8+2 | |
| ⇓ | ⇓ | |
| 10 | 10 |
At this point, don't worry about BODMAS's Order; that's covered in BIDMAS, below. It's the other five in the list that you're most likely to be concerned with when you create formulas in your spreadsheets.
Excel and BODMAS
Excel adheres to the BODMAS rule of arithmetic. Yet you have to be careful about how you explain to Excel exactly what it is you want it to calculate.
Back to oranges and apples: six oranges and nine apples to be shared between three girls and two boys so that each kid gets the same number of pieces of fruit. And where we started:
six plus nine divided by three plus two
In evaluating 6 + 9 / 3 + 2 BODMAS indicates do the division first, effectively reducing the expression to 6 + 3 + 2, before completing the calculation by addition to get the result of 11:
| 6+9/3+2 |
| ⇓ |
| 6+3+2 | ⇓ |
| 11 |
With your brain now comfortably accommodating BODMAS and its two conditions, using brackets you instruct Excel to add the six and nine together, and the three and two together, before doing the division.
( six plus nine ) divided by ( three plus two )
Hence, following BODMAS:
| (6+9)/(3+2) |
| ⇓ |
| 15/5 |
| ⇓ |
| 3 |
In Excel speak:
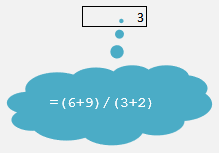
An equals sign at the start of an entry in a cell in an Excel spreadsheet indicates to Excel that the cell contains a formula that Excel must evaluate.
Best Practice
Ordinarily, in your use of Excel you wouldn't embed the expression in a single cell, as illustrated above. You'd have cells to hold the data and a cell for the formula.
You'd construct your formula according to BODMAS using references to the cells that contain the values your formula is to work upon:
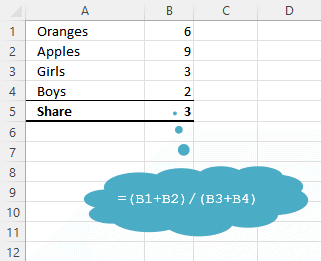
Always check your formula before letting it go live. Using easy numbers is one way of testing that it's working properly.
More About Excel and Brackets
Sometimes there is more than one way to apply brackets to achieve the correct result using Excel. Take the calculation of Emma's expense allowance for her use last year of her own car for business.
Emma drove a total of 7,000 miles in the year, accompanied for 1,500 of those by a passenger.
Emma is allowed 45p for each mile driven and 5p for each mile in which a passenger is on board.
Before our appreciation of BODMAS we might mistakenly have tried this (the division by 100 intended to convert pence p to pounds sterling £):
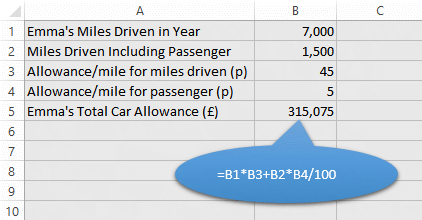
Now we know how Excel has completed the illustrated formula accoding to BODMAS:
- 7000*45 (B1*B3) to give 315000
- 1500*5/100 (B2*B4/100) to give 75
- 315000+75 to give 315075.
To put things on track, we need to decide at what point we're going to convert pence to pounds (or cents to dollars). We could do this as we go along without recourse to any brackets:

Or in this instance including brackets:

In this instance, we've totalled up all the allowances in pence and before dividing by 100 to get to pounds.
And So to BIDMAS
MJW informs me that she was taught BODMAS in primary school and in secondary school until it mutated into BIDMAS. That was when indices became a main topic in maths.
The index (the I in BIDMAS) of a number, also referred to as the power of a number.
I'm guessing that if you're into indices, then you're well into you maths and don't need me to explain them here.
If you're not, then I'm copping out of taking responsibility for your further education. Plenty of good tuition on the web in pursuit of your homework.
Mental Preparation
If your life is too short to waste time fretting over an Excel formula that isn't working as you want it to, then I have a routine to recommend:
- Make sure you're clear in your mind what your formula has to do. By that I mean tell yourself about it; even scribble a note
- Turn away from your spreadsheet. Consider that in completing step #1 you've taken positive action
- Take a break from the spreadsheet: don't give it another thought — answer some emails, complete some other task, have a coffee, go for a stroll, take a power nap. Even go to bed and leave things until tomorrow
- Return to the formula and try out any fresh approaches that now may have come to mind
- If none of these work, then ask for help, or search the web or, if time is not pressing for a result, then repeat the cycle.
What I'm suggesting here is that you enlist your subconscious in the pursuit of your formula.
“Think of your subconscious as the back-office of your brain, dealing with all the deep tasks, while your conscious mind cooks dinner, navigates through traffic, chooses which Netflix show to watch, and holds a conversation. Ever notice all the green cars after you buy a green car, or you take out the trash and a great idea pops in your head from nowhere? This is your subconscious hard at work in the background.”
How to Engage Your Subconscious Mind to Solve Your Toughest Problems
August Birch, 2018-09-07.
If your formula is proving elusive, you may need to follow the routine more than once — to leave your subconscious time to incubate the problem.
“She [Professor Sarah Gilbert] likes to go for walks when thinking through problems—‘It helps to activate the brain,' she says.”
The race to save the world
The Sunday Times Magazine, February 21 2021
Your subconscious may not deliver a solution at a time that's convenient. Mine popped me the solution to a by-then two-week-old problem whilst I was concentrating on getting in the correct lane for the slip road onto the M4 east-bound at Junction 8/9.
Your Support for DMW TIPS
Please support this website by making a donation to help keep it free of advertising and to help towards cost of time spent adding new content.
To make a contribution by PayPal in GBP (£ sterling) —
To make a contribution by PayPal in USD ($ US) —
Thanks, in anticipation.
